Be warned: this one will hurt your mind a little. This is the Monty Hall Problem, a mathematical solution to a question of probabilities which led to division and acrimony in the math community.
Inspired by a popular US TV show and named after its presenter, few other math problems have become as well known. For those uninitiated let us introduce you to the sometimes confusing world of probability, and unveil the secrets behind the Monty Hall Problem.
Why did so many mathematicians find it hard to accept a solution that seems too good to be true?
Controversial Mathematics
The Monty Hall Problem can be traced back to the popular American game show called “Let’s Make a Deal,” hosted by Monty Hall from 1963 until 1991. Understanding the concept of the show is central to understanding the problem.
The show was made up of different segments, and the one we are interested in involves a contestant being presented with three doors. One typically had a high-ticket prize behind it, like a fancy new car, while the other two hid something a little less desirable, a booby prize (typically something like a goat).
The contestant’s task appeared simple: select a door and hope to reveal the grand prize. There was a twist, however.

Once the contestant had made their choice, Monty Hall, who knew what was hidden behind each door, would open one of the remaining doors that didn’t have the grand prize behind it. Monty’s door therefore always revealed a goat.
Once there were only two doors remaining, the contestant was offered a choice of the two remaining doors. The question then became, should the contestant stick with their original choice or switch to the other unopened door? The show cleverly played on some people’s natural instinct to second-guess themselves, and on the unwillingness of others to change their minds.
- The Hole in Pascal’s Wager: A Flawed Thought Experiment?
- “And Yet It Moves” – Galileo, the Planets, and the Church
But, honestly, it seems pretty straightforward, doesn’t it. You have two doors left, one with a car and one with a goat, which fairly obviously presents a fifty/fifty split as to which you get. But what if we told you it isn’t fifty/fifty?
The Monty Hall Problem gained widespread attention in the early 1990s when a reader named Craig F. Whitaker wrote a letter to Marilyn Vos Savant, who was famous for her “Ask Marilyn” column in Parade magazine, laying out his conundrum. Was it better to stick with one’s original choice or not?
In her response, Vos Savant explained the counterintuitive solution, arguing that the contestant should always switch doors to maximize their chances of winning the grand prize. Despite her clear explanation, the problem continued to baffle many, including some mathematicians, leading to spirited debates.
The Math Behind the Problem
At its heart, the Monty Hall Problem is a fascinating probability conundrum. Not all of us have mathematics degrees so let’s try to break it down without delving too deep into complex formulas.
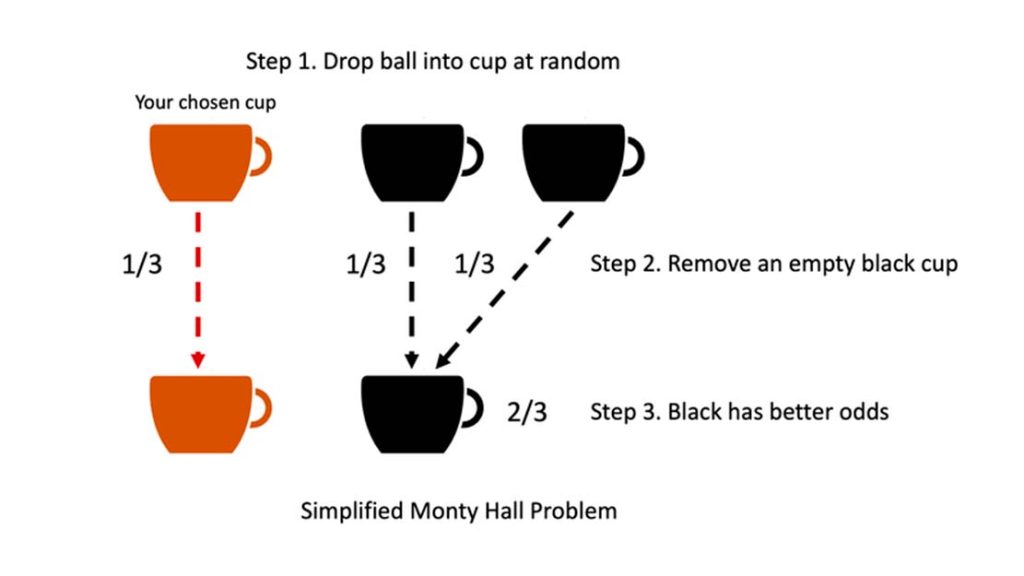
When the contestant initially chooses a door, there’s a one-in-three chance (33.33%) of picking the door with the grand prize and a two-in-three chance (66.67%) of selecting a door with a goat.
The twisting of the probabilities comes when Monty removes one of the doors, always with a goat behind it. When he opens a door with a goat, the fact that he always has to choose a goat provides us with valuable information.
If the contestant’s first choice was a goat door (a 66.67% chance), Monty has no choice but to reveal the other goat door. However, if the initial choice was the grand prize door (a 33.33% chance), Monty can reveal either of the two goat doors.
When the contestant decides to switch doors after Monty’s reveal, they are essentially betting that their initial choice was a goat door (unless they just really like goats). Statistically speaking, the chances are two-thirds (66.67%) that their first pick was a goat.
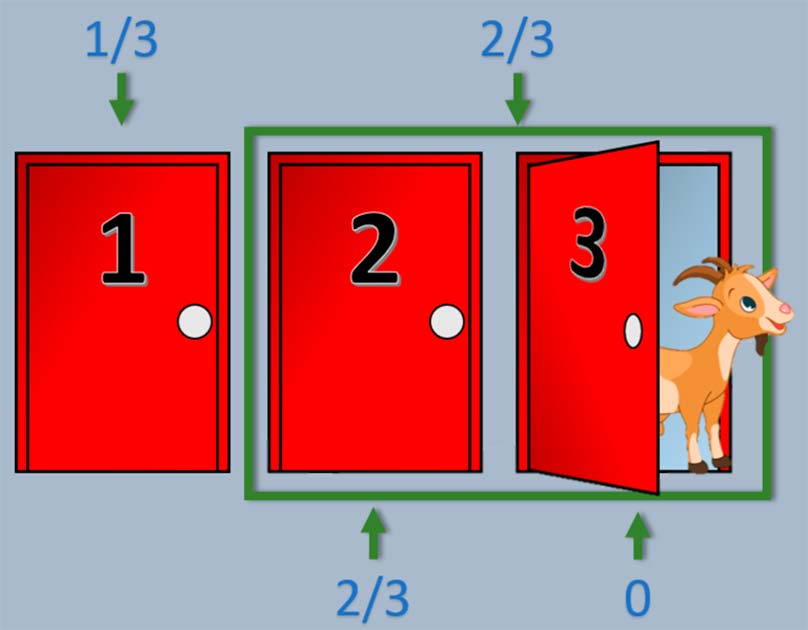
Therefore, switching increases the likelihood of winning the grand prize to two-thirds, while sticking with the original choice only gives a one-third chance. Though it might defy our intuition, the math is clear—switching doors offers the best odds of winning.
The Controversy
So, so far, not too complicated, right? But after Vos Savant’s column was published in Parade magazine in 1990 her answer proved to be incredibly controversial.
The publication was inundated with over 10,000 complaints, 1,000 of those written by Ph.D. holders claiming that Savant was wrong. Even after being given proper explanations, simulations, and formal mathematical proof many people still refused to believe Savant was correct. But why?
The reason behind this lies in the clash between intuition and the logic of probability. Our intuition often leads us astray in this scenario because we tend to assume that when Monty reveals one of the goat doors, it has no bearing on the probability of the remaining doors.
We might think, “Since there are only two doors left, the chances of winning should be 50-50, regardless of whether we switch or not.” This common misconception is known as the “equal probability fallacy.”
However, the key to understanding the Monty Hall Problem is recognizing that Monty’s actions are not random. He strategically opens a door with a goat behind it, and his choice is constrained by the rule that he can’t reveal the grand prize. This non-random aspect of the problem is what alters the probabilities.
Another reason for the controversy is that human beings are generally averse to change and tend to stick with their initial choices, even when presented with evidence suggesting otherwise. This psychological phenomenon is called “cognitive dissonance,” where individuals experience discomfort when faced with conflicting beliefs (for example, their initial choice might be wrong).
This has all led to the Monty Hall problem being described as a veridical type of paradox. This is because its solution is so counterintuitive to the human instinct that it seems absurd despite being demonstrably true. In this way, it is similar to much older problems like the Three Prisoners problem and Bertrand’s Box paradox.
In conclusion, the Monty Hall Problem stands as a quirky yet fascinating puzzle that challenges our intuitions and illuminates the intriguing world of probability. Though it has sparked spirited debates and confounded many, its mathematically sound solution prevails.
The counterintuitive nature of the problem serves as a valuable lesson, reminding us to question our assumptions and embrace the logic of probabilities. So, the next time you encounter three doors and a cunning host, remember to switch confidently, for you’ll be harnessing the power of probability and mastering the enigmatic Monty Hall Problem like a seasoned gameshow strategist.
Top Image: The Monty Hall Problem is a great example of the sometimes counterintuitive nature of probability. Source: Romana / Adobe Stock.